Mechanical Properties
The way a material responds to external forces acting upon it, in terms of its mechanical behavior, plays a crucial role in civil engineering and construction. Every material, when subjected to loads, undergoes deformation; however, the specific manner in which it responds to these loads is influenced by its inherent mechanical properties, the nature of the applied loads, and the geometric configuration of the structure. Evaluating mechanical properties is essential for the design and planning of projects that ensure the safety and integrity of built structures.
The concept of “failure” of a material is linked to its ability to withstand applied loads. The definition of failure can vary based on different evaluation criteria. In obvious cases, failure leads to catastrophic material fracture, resulting in the complete failure of a structural element and the potential collapse of the entire structure. However, in less visible situations, the consequences of failure can be equally severe. For instance, a pavement surface might exhibit excessive roughness, which could be considered a failure even if the material’s strength properties are adequate. In this regard, considering the geometry and functionality of materials is crucial in defining the limits of acceptable performance.
In civil engineering, buildings, bridges, roads, and other infrastructures are designed to resist and withstand various loads, whether static loads like the structure’s own weight or dynamic loads such as wind, vehicular traffic, and seismic forces. Understanding the mechanical properties of materials used in these constructions is crucial to ensure that the structure can safely and effectively withstand all these forces. For example, selecting high-strength steel for bridge beams would allow the bridge to support heavy loads without excessive deformation.
In addition to load resistance, the deformation a material undergoes under these forces is also considered. Elasticity is one of the most important mechanical properties; an elastic material is one that can deform temporarily under load and then return to its original shape when the load is removed. This property is essential in structures subjected to cyclic or repetitive loads, as it prevents the accumulation of permanent deformations.
Importance in Structural Design
In terms of structural design, knowledge of mechanical properties is essential to determine a material’s load-carrying capacity and, consequently, the amount of material needed to ensure the safety and durability of a structure. If a material’s mechanical properties are insufficient to withstand the anticipated loads, it may result in an unsafe design and the need to reinforce or redesign the structure, potentially increasing costs and delaying the project.
The mechanical properties of materials used in civil engineering and construction have a significant impact on the behavior and durability of structures. Understanding how materials respond to external loads and deform under different conditions is essential for the successful design, planning, and execution of civil engineering projects, ensuring the safety and optimal performance of built infrastructures.
Response to Loads
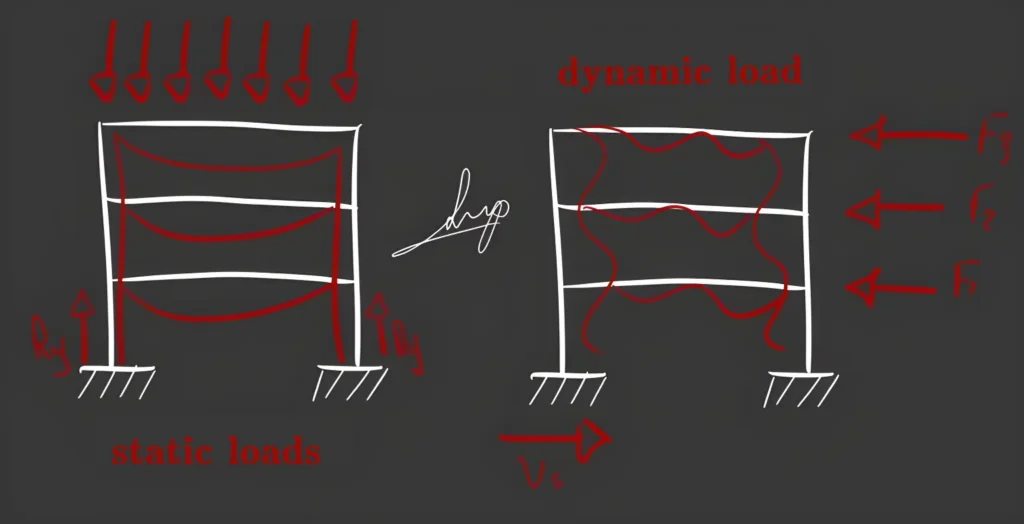
Load conditions play a fundamental role in material analysis in civil engineering, determining how materials will respond to different types of forces and loads throughout the lifespan of a structure. These conditions directly influence the selection of materials and the design of structural elements to ensure the safety, durability, and functionality of constructions.
In civil engineering, there are two main types of loads: static loads and dynamic loads. Static loads are constant or slowly applied forces on a structure and can include the structure’s own weight, permanent loads like walls and equipment, and temporary loads like occupancy load. These loads act gradually and steadily, allowing materials to adjust to the forces without significant vibrations.
On the other hand, dynamic loads generate vibrations or movements in the structure. These can be periodic, such as those generated by rotating equipment, or random, such as those caused by earthquakes. Dynamic loads can also be transient, such as those generated by vehicles passing over a bridge. These loads pose additional challenges to materials, as they must withstand fluctuations in forces and vibrations, which can lead to fatigue or premature deterioration.
An example of a static load would be the self-weight of a building and its permanent contents, such as walls and HVAC systems. In contrast, an example of a dynamic load would be wind generating vibrations in a bridge or seismic loads during an earthquake. Careful consideration of these load conditions allows engineers to choose the right materials and design structures optimally to resist the forces to which they will be exposed, ensuring safety and integrity over time.
Stress-Strain Curve

The stress-strain relationship is an essential feature in material analysis in civil engineering, describing how materials respond to applied forces. This relationship quantifies the relationship between the force exerted on a material and the resulting deformation. Since Robert Hooke’s early discoveries in 1678, it has been observed that, within certain limits, the deformation of a material is proportional to the applied force, resulting in a linear relationship. By collecting data from tension and compression tests conducted in materials strength laboratories, we can calculate many details about these mechanical properties and load-carrying capacity of each material.
This relationship is mathematically described through two key parameters: stress and strain. Stress is the force applied per unit area (Force/Area), and strain is the change in length divided by the original length (Change in length/Original length). The stress-strain curve, representing these two parameters, provides essential information about the mechanical properties of a material and its behavior under loads.
The stress-strain relationship is crucial for the design and analysis of structures in civil engineering. It allows predicting how different materials will respond to the loads and forces they will undergo during their lifespan. The stress-strain curve for a particular material can provide crucial information about its mechanical properties, such as its yield point, elastic modulus, proportional limit, and ultimate strength. This information is vital for determining if a material is suitable for a specific application and for ensuring the safety and durability of built structures.
Elasto-Plastic Mechanical Properties
The elastoplastic behavior of materials in civil engineering refers to the ability of certain materials to undergo both elastic and plastic deformation under applied loads. Unlike elastic behavior, where materials recover their original shape after loading, elastoplastic behavior involves permanent deformation after a certain point, even if the load is removed. This combination of elasticity and plasticity is characteristic of many materials used in construction, such as steel and reinforced concrete.
The importance of elastoplastic behavior lies in its relevance to the design and analysis of structures in civil engineering. By understanding how materials behave under different load levels, engineers can ensure that structures are safe and durable. For example, in the design of bridges and buildings, it is essential to consider how materials will deform and withstand loads over time. Elastoplastic behavior is also crucial to prevent catastrophic failures in structures, as it provides information on how materials will deform before reaching their strength limit.
The ability of materials to undergo elastoplastic deformation allows engineers to design structures that can absorb energy and redistribute loads effectively. This is especially important in situations such as earthquakes, where loads change rapidly and may exceed static load levels. By understanding and accounting for the elastoplastic behavior of materials, engineers can design resilient structures that can withstand variable loads and provide a safe and controlled response under different load conditions.
Elastic Behavior of Materials
When addressing the concept of elastic behavior of materials, we know that this is one of the mechanical properties referring to the ability of certain substances to react instantly to an applied load, returning to their original shape upon removing this load. This elastic response is especially characteristic in a wide range of materials, including most metals, particularly at low stress levels. During elastic deformation, the arrangement of atoms composing the material does not undergo substantial modification; rather, there is stretching in the existing atomic bonds. Once the load is removed, these bonds return to their initial position. A pioneer in studying this relationship was Thomas Young, who noted that different elastic materials exhibit various proportionality constants between the applied stress and the resulting deformation. See Young’s Modulus or Elastic Modulus.
In the context of an axial tension test, where a material is subjected to tensile force, its elongation results in a reduction in the cross-sectional area in the lateral direction. In contrast, in the axial compression test, involving a compressive load, the opposite phenomenon occurs. An essential relationship is known as Poisson’s ratio, linking lateral deformation with axial deformation. This ratio is expressed with a negative sign because axial and lateral deformations always have opposite signs. Poisson’s ratio has a theoretical range from 0.0 to 0.5. A value of 0.0 would reflect a compressible material where axial and lateral directions do not interfere, while 0.5 would indicate a material that does not experience volume change under load. In practice, most solids have Poisson’s ratio values between 0.10 and 0.45, suggesting some influence between axial and lateral directions during elastic deformation.

Work and Energy in Material Assessment
When subjecting a material to strength tests, a testing machine is used to generate a force to move or deform the material. Since work is calculated by multiplying force by distance, the area under the force-displacement curve represents the work done on the object. By dividing force by the material’s cross-sectional area to obtain stress and dividing the change in length by the original length to obtain strain, the force-displacement graph transforms into a stress-strain graph. However, the area under this graph is no longer expressed in work units. By manipulating the units of the stress-strain graph, we can deduce that this area is equivalent to the work per unit volume required to deform or break the material. This concept is valuable when selecting materials for situations where they need to absorb energy.
For example, the area under the elastic part of the curve is called the resilience modulus. The energy required to fracture a material is indicative of its toughness, emphasizing that high strength does not automatically guarantee toughness. For example, increasing the carbon content in steel raises its yield strength but reduces its ductility. This results in an increase in strength, although it may decrease toughness.
Temporary Response in Material Deformation
Our previous analysis assumed that deformation was an instantaneous response to stress, a valid assumption for elastic materials. However, this is not the case in all situations, as some materials exhibit a delayed response depending on their mechanical properties. The amount of deformation depends on the duration of the load, temperature, and material properties. Various mechanisms are associated with this temporary deformation, such as creep and viscous flow. Although these terms are not clearly distinguished, creep is usually applied to long-term deformations, while viscous flow is related to amorphous materials and can occur with short-duration loads. Examples include concrete, susceptible to creep over decades, and asphalt pavements with viscous flows caused by traffic in fractions of a second. Creep in metals is less relevant in civil engineering. In steel, it can occur at temperatures above 30% of its absolute melting point, affecting the design of nuclear reactors and boilers.
Rheological Modeling of Mechanical Behavior
Rheological models are used to mechanically describe the temporary behavior of materials, especially polymers characterized by various forms of deformation. These materials can be modeled by combining simple physical elements used in rheology. Three fundamental elements in rheology are Hooke’s element, Newton’s element, and St. Venant’s element, which can be combined in series or in parallel to represent complex behaviors.
Effects of Temperature and Time on Mechanical Behavior
Temperature affects the mechanical behavior of all materials, although some are more sensitive than others. Viscoelastic materials, such as plastics, are strongly influenced by small temperature variations. In contrast, metals and concrete are less affected near room temperature, although ferrous metals can become brittle below their transition temperature. The duration of the load also influences, similar to temperature. Viscoelastic materials are affected by the rate of load application. For example, an asphalt pavement will not show permanent deformations under a high-speed truck but will under the same truck parked on a hot day.
Failures and Safety in Materials and Structures
Failures occur when an element or structure cannot fulfill its intended function. Failure modes include fatigue fracture, general yielding, buckling, and excessive deformation. Fracture is a common failure, occurring abruptly in brittle materials and through plastic deformation in ductile materials. Repeated loads can cause fatigue in structures, even below the material’s strength. Ferrous materials have a fatigue strength limit, usually between a quarter and half of the material’s strength. Examples of failures include bridges and pavements, where repeated loads cause fatigue cracks.
Conclusion
The mechanical properties of each material can vary significantly, and depending on these properties, engineers must identify whether the material meets the requirements or is capable of fulfilling the function for which it was intended; the study of mechanical properties is one of the most important fields for materials engineering, as it will facilitate the work for virtually the rest of the engineering disciplines.
About The Author
Samuel Parariá
Estudio: University of Francisco de Paula Santander.
Major: Civil Engineering.
Favorite Areas: Structures, Traffic Engineering, and Road Design.
Location: Cúcuta, Norte de Santander, Colombia.






Related
Pavers in Civil Engineering
What are the Non-Mechanical Properties of Materials in Civil Engineering?
Ecological Bricks: The Future of Sustainable Construction